Checkerboard分解
对于某些e指数上的矩阵,如前文所提到的最近邻的hopping矩阵,或者类似形式的辅助场的矩阵,我们通常将其分为不同的family,每个fammily里是互相对易(分块)的小矩阵,这样利用了矩阵的稀疏的性质,方便进行矩阵的 $\exp$ 的运算,以及进行矩阵乘法。
以 $4 \times 4$ 晶格的最近邻hopping为例:
\begin{aligned}
e^{-\Delta \tau \hat{T}} &=\prod_{\sigma} e^{-\Delta \tau t \sum_{\langle i j\rangle}\left(\hat{c}_{i \sigma}^{\dagger} \hat{c}_{j \sigma}+\hat{c}_{j \sigma}^{\dagger} \hat{c}_{i \sigma}\right)} \\
&=\prod_{\sigma} e^{-\Delta \tau t\left[\sum_{\langle i j\rangle \in \operatorname{fam}_{1}}\left(\hat{c}_{i \sigma}^{\dagger} \hat{c}_{j \sigma}+\hat{c}_{j \sigma}^{\dagger} \hat{c}_{i \sigma}\right)+\sum_{\langle i j\rangle \in \mathrm{fam}_{2}}\left(\hat{c}_{i \sigma}^{\dagger} \hat{c}_{j \sigma}+\hat{c}_{j \sigma}^{\dagger} \hat{c}_{i \sigma}\right)\right]} \\
& \approx \prod_{\sigma} e^{-\Delta \tau t\left[\sum_{\langle i j\rangle \in \operatorname{fam}_{1}}\left(\hat{c}_{i \sigma}^{\dagger} \hat{c}_{j \sigma}+\hat{c}_{j \sigma}^{\dagger} \hat{c}_{i \sigma}\right)\right]_{e}-\Delta \tau t\left[\sum_{\langle i j\rangle \in \mathrm{fam}_{2}}\left(\hat{c}_{i \sigma}^{\dagger} \hat{c}_{j \sigma}+\hat{c}_{j \sigma}^{\dagger} \hat{c}_{i \sigma}\right)\right]} \\
&=\prod_{\sigma} \prod_{m=1}^{2} \prod_{n=1}^{N / 4} e^{-\Delta \tau (-t)\sum_{\langle i j\rangle \in \square_{m n}}\left(\hat{c}_{i \sigma}^{\dagger} \hat{c}_{j \sigma}+\hat{c}_{j \sigma}^{\dagger} \hat{c}_{i \sigma}\right)}
\end{aligned}
\end{equation}\]
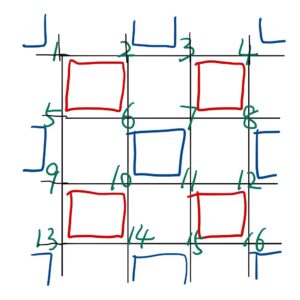
如下图所示,两个family分别为红色和蓝色。可以看到比如不同的红色方块之间没有共有的site,即其是互相对易(分块)的,而每个方块是形如:
\begin{pmatrix}
0 & -t & 0 &-t \\
-t &0 & -t & 0\\
0& -t & 0 & -t\\
-t & 0 & -t & 0
\end{pmatrix} \end{equation}\]
的矩阵,我们只需对这个矩阵对角化算其 $\exp$ ,得到 $4 \times 4$ 的矩阵们。包括之后进行矩阵乘法,也可以拿不同的 $4 \times 4$ 矩阵分别和大矩阵分块的乘起来。
Self-learning Monte Carlo
我们知道,对于某个具体的玻色子的构型,能算出有对应的权重$W$。而对于一个经典的只有玻色子的哈密顿量,我们有 $W=e^{-\beta H}$
在有费米子存在的情况下,我们的权重和某个行列式有关,而无疑计算行列式是一件很耗时的事情,一个自然的想法是,既然我们在采样的时候,是对于辅助场(玻色子)的构型空间进行采样(费米子部分都分别trace掉了),那如果我们找到只含玻色子的有效哈密顿量,则只需要计算前后玻色子的能量差即可。即我们期望的是:
W=e^{ -\beta H[\mathcal{C}]}=\operatorname{Det}\left[\mathbf{I}+ \mathbf{B}_{C}^{\sigma}(\beta, 0)\right] \longrightarrow W=e^{-\beta H^{\mathrm{eff}}}
\end{equation}\]
但严格的等价是很难办到的事情,但我们能够近似的找到一个有效哈密顿量 $H^{\mathrm{eff}}$ ,使得 $\qquad $ $\operatorname{Det}\left[\mathbf{I}+ \mathbf{B}_{C}^{\sigma}(\beta, 0)\right] \approx e^{-\beta H_{eff}}$ 。
比如我们可以将有效哈密顿量的形式假设为参数为 $J_1$ 的最近邻的伊辛模型,或是还有次近邻 $J_2$ 次次近邻 $J_3$ ...的伊辛模型。而这些参数的取值,则可以通过不同构型所对应的权重,来学习。这个过程可以用各种机器学习的方法。
对于某构型 $x_i$ ,对应的权重为 $W_i$ ,我们通过调整各参数 $J$ 的值,使得
$W_i \approx e^{-\beta H^{\mathrm{eff}}(x_i)}$
在有了有效哈密顿量之后,我们就能够用有效哈密顿量所对应的权重进行更新。但这样的更新和实际的更新是会有所差别的,所以我们在用有效哈密顿量对应的权重进行蒙卡的更新若干步后,最后要按照原哈密顿量,算一下更新最初和更新后的权重比,多一个接受概率,来把总的接受概率修正到满足细致平衡条件,该接受概率为:
A\left(\mathcal{C} \rightarrow \mathcal{C}^{\prime}\right)=\min \left\{1, \frac{\exp \left(-\beta H\left[\mathcal{C}^{\prime}\right]\right)}{\exp (-\beta H[\mathcal{C}])} \frac{\exp \left(-\beta H^{\mathrm{eff}}[\mathcal{C}]\right)}{\exp \left(-\beta H^{\mathrm{eff}}\left[\mathcal{C}^{\prime}\right]\right)}\right\}
\end{equation}\]
顺便,通常的经验是,在某个温度和size学到的有效模型(比如学到了 $J_1$ 的值),可以套用到同样温度稍大一些的size。
