由于每次更新格林函数都是在原有格林函数的基础上进行累积更新，并且需要在不同虚时上进行传递，数值误差的积累会越来越大。格林函数的计算涉及到的是矩阵运算，其数值误差增长的快慢与 $B$ 矩阵的范数有关。一个矩阵的范数指的是最大奇异值和最小奇异值的比值，对于无相互作用系统， $B$ 矩阵的范数就是 $\exp(\beta W )$ ，其中 $W$ 为能带最高与最低能量之差，即带宽。而对于相互作用体系，一般来说， $\beta$ 越大，相互作用强度越大， $B$ 矩阵的范数就越大，这点我们在数值计算中已经验证过。

在大 $U$ 或是 $\beta$ 很大的时候，计算格林函数就会有很大的数值稳定的问题，其原因在于...各矩阵的范数/condition number过大，在矩阵相乘的时候，大的和小的scale混在一起。我们有很多已经被证明是weakly backward stable的算法

对于格林函数的求解，等价为解线性方程组：

我们定义condition number为矩阵和矩阵的逆的范数的乘积：

该量大概的和矩阵最大奇异值与最小奇异值的比值有关，与矩阵乘法误差的上界有关。

因为condition number过大，所以我们得到的解的相对误差：

会非常大。其中 $\epsilon_{\mathrm{m}}$ 是机器的unit round off 误差，IEEE单精度是 $\epsilon_{\mathrm{m}}=2^{-24}$，IEEE双精度是 $2^{-53}$ 。某些情况下 $\epsilon_{\mathrm{m}} \kappa\left(I_{n}+B_{L} \cdots B_{2} B_{1}\right)$ 很容易就比1还大，这意味着你的解可能一位有效的都没有。

数值稳定的具体操作如下。

先回忆一下定义：

其中 $\pm$ 对应自旋上下， $\cosh (\alpha)=e^{\Delta \tau U / 2}$ ， $\operatorname{Diag}\left(\vec{S}_{l}\right)$ 表示对角元分别为 $s_{i, l}=\pm 1$ 的矩阵， $T$ 为只在
最近邻处有矩阵元 $-t$ 的矩阵。

为了避免数值稳定的问题，我们不妨每隔 $\tau_1$ 做一次数值稳定，$\tau_1$ 的选取使得 $B_{C}\left(n \tau_{1},(n-1) \tau_{1}\right)$ 不超过机器精度。而 $B_{C}(\tau, 0)=B_{C}\left(n \tau_{1},(n-1) \tau_{1}\right) \cdots B_{C}\left(\tau_{1}, 0\right)$ ，我们做数值稳定的第一步是得到 $B_{C}(\tau, 0)$ 或 $B_{C}(\beta,\tau)$ 的对应的UDV矩阵（注意，不是直接对这些矩阵进行奇异值分解），以 $n=3$ 为例子：

通过如此的方法，我们能得到 $B_{C}(\tau, 0)=U_{R} D_{R} V_{R}$ ，类似的，对于 $B_{C}(\beta, \tau)$ ，同样的有 $B_{C}(\beta, \tau)=V_{L} D_{L} U_{L}$ （注意之前是UDV，现在是VDU，之前是从右往左逐步做奇异值分解得到，现在是从左往右）。

实际上经常选择做 modified Gram-Schmidt (MGS)。其中 $U$ 是正交的， $D$ 是对角的， $V$ 是单位上三角阵。总之，我们的目的是，希望 $U$ 和 $V$ 的性质都很好（这样的矩阵，矩阵乘法的性质很好），只有 $D$ 矩阵的condition number很大。或者QR分解/LQ分解。

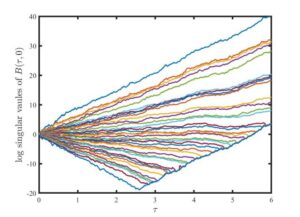
事实上，如果不进行逐步的SVD，或者是使用某些算法实现的SVD，可以看到数值不稳定的迹象之一： $B(\tau,0)$ 所得到的包含奇异值的各个$D$矩阵，即所对应的奇异值，在$\tau$很大的时候，会有奇异的现象如图（arXiv:2003.05286 ），即较小的奇异值会上升且数值变的相同（如图为 $U=6, L=6, \Delta \tau=0.01$ ，使用matlab自带的svd函数进行数值稳定的结果）：

在此基础上，有诸多方法计算格林函数：

方法一

已知：

且有：

则：

得到的矩阵的右下角即为 $G(\tau,\tau)$

方法二

方法三

此方法为我们实际上用的方法（分为用QR分解的和SVD分解（或modified Gram-Schmidt (MGS) factorization）的等等）：

SVD（或modified Gram-Schmidt (MGS)factorization）

第三个等号White等人当年也这么建议。

上式其中： $D_{L}^{\max }(i,i)= \max \left\{ D_{L}(i,i),1 \right\}$，$D_{L}^{\min }(i,i)= \min \left\{ D_{L}(i,i),1 \right\}$

类似的，有：

以及：

还有：

QR

其余情况不再举例。

总之总之，我们希望做的事情就是尽可能的将大的scale和小的scale分离，仅仅在最后才将他们mix在一起。

大致流程

在代码中，我们实际只需要一套UDV的变量存在，在更新到第 $\tau$ 层时，我们分别有一半的 $ U_{R} D_{R} V_{R}$ 和一半的 $V_{L} D_{L} U_{L}$ 。注意到等时格林函数需要的是两边的 $B(\tau, 0) $ 和 $B(\beta, \tau)$ 的UDV矩阵。

比如最初先得到所有的 $B(\tau, 0) $ 对应的UDV矩阵。然后从第 $\beta$ 层逐层更新辅助场，则只需要逐步的得到到第 $\tau$ 层为止的 $B(\beta, \tau)$ 所对应的VDU矩阵即可。

符号问题

我们知道，在进行量子系统的模拟时，我们实际上将其转化为了经典的概率分布，来进行蒙卡的采样。而实际上对于行列式蒙卡来说，各个辅助场构型所对应的权重为某个矩阵的行列式，如果没有任何限制，一个行列式的值自然可能是负数甚至是复数，如果对应的权重不是正的实数，如此我们就无法进行马尔科夫蒙特卡洛的计算（因为权重比和我们的接受概率有关，一个负的或复的接受概率，我们无法继续进行计算）。

值得注意的是，符号问题的产生decouple的方式有关，同样的也和计算是basis的选取有关（显然如果选取能量的本征态，就没有符号问题）。符号问题是一个NP-hard的问题，即不存在符号问题的通用的一般解决方案。

下面简单介绍两类，对于部分情况下，没有符号问题的证明：

情况一

如果一个系统有着反幺正对称性存在，则系统没有符号问题。

反幺正变换的性质见附录

具体的表述为，如果存在一个反幺正变换$\mathcal{K}$，使得：

则费米子部分的权重相关的矩阵 $1+B_{C}(\beta, 0)$ 的本征值成对出现（即有本征值 $\lambda_i$ ，则相应的有对应的另一个本征值，其共轭 $\lambda_i^{*}$ ），即 $\det \left( 1+B_{C}(\beta, 0) \right) =\prod_i |\lambda_i|^2$ 。
上式其中 $T$ 和 $V(\boldsymbol{s})$ 分别为动能项和decouple之后的相互作用项。

对于权重对应矩阵 $1+B_{C}(\beta, 0)$ ，假设有本征值 $\lambda$ ，对应本征向量为 $\mathcal{V}$ ，我们有：

因为有 $\mathcal{K}(1+B(\beta, 0)) \mathcal{K}^{\dagger}=(1+B(\beta, 0))$ ，则：

显然 $\lambda^{*}$ 也为其本征值。由反幺正变换的性质，我们有：

我们知道 $\mathcal{V}$ 和 $\mathcal{K} \mathcal{V}$ 是正交的，即 $\lambda$和$\lambda^{*}$ 是不同本征向量所对应的本征值。

而对于如下的哈密顿量：

我们注意到上的部分在反幺正变换下，变成下的部分：

则下的部分的权重与上的部分互相共轭，实际只需要算上部分的权重（比），不需要再计算下部分的权重（比）。

情况二

而对于诸如Hubbard model，情况略有不同。比如我们只能算$U>0$的半满的情况，是因为我们有着诸如下面的幺正的Particle-hole变换（仅在bipartite lattice是well-defined的）保证的：

hopping项不变，而对于decouple到不同channel的部分：

$S_z$ Channel $\alpha$ 是实的，单看变换前的结果，是看不出是否有负符号问题存在的。而在Particle-hole变换之后，我们看到对于自旋上和下是相同的，最终权重应该是上的部分的平方，在乘上一个实的$\exp$型的因子，所以自然没有负符号问题（所有矩阵元素都是实的就更不会有复符号问题了）。

CDW Channel $\alpha$ 是虚的，单看变换前的结果，是看不出是否有复符号问题存在的。而在幺正的Particle-hole变换之后，权重的值是不变的。我们看到对于自旋上和下的各矩阵元素都是互相复共轭的，Particle-hole变换之后权重为正的实数，权重自然为正的实数。